Introduction to Newton-Raphson method
Newton-Raphson method 是一种在实数域和复数域上近似求解方程的方法,该方法利用函数 $f(x)$ 的泰勒级数的前几项来求 $f(x) = 0 $ 的根。
Theory
欲求连续可微函数 $f(x) = 0$ 的根,步骤如下:
-
假设 $x_0$ 为根附近的任一点,$f(x)$ 在 $x_0$ 的泰勒展开式如: $$ f(x) = f(x_0) + f’(x0)(x-x_0) + 1/2 f’’(x_0)(x-x_0)^2 + … = 0 $$ 以上 $f^\prime(x)$ 为一阶导数,$f’’(x)$ 为二阶导数,依次类推。
-
假设 $x - x_0$ 足够小,则泰勒展开式中只前几项对函数对求根的较为重要,在展开式第二项截断,令$f(x) = 0 $,我们可得: $$ x_{1}=x_{0}-\frac{f\left(x_{0}\right)}{f^{\prime}\left(x_{0}\right)} $$ 以上$f^{\prime}\left(x_{0}\right)$ 为 $f(x)$ 在 $x_0$ 的切线,$x_1$ 即为切线与 $x$ 轴的交点,$ x_1 $ 即为新的根估计值。
-
依次做上述迭代,直至 $x_(i + 1) - x_i$ 收敛至给定误差范围 $\epsilon$, $$ x_{i+1}=x_{i}-\frac{f\left(x_{i}\right)}{f^{\prime}\left(x_{i}\right)} $$ 收敛的充分条件为:若 $f(x)$ 二阶可导,那么欲求的根 $x$ 周围存在一个区域,只要初始点 $x_0$ 在该区域内,那么该方法一定收敛。
Limitations
-
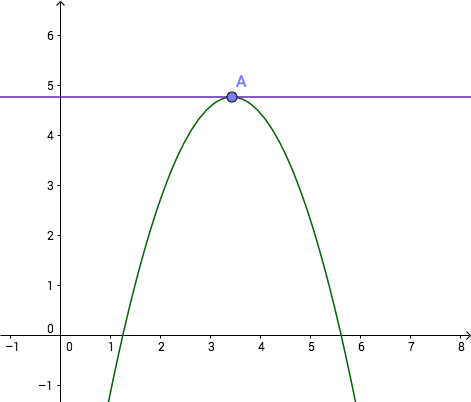
如果起始点选取了驻点,则牛顿法可能不起作用。
代数上,由于$ f^\prime(x) = 0 $ , $x_{i+1}=x_{i}-\frac{f\left(x_{i}\right)}{f^{\prime}\left(x_{i}\right)}$ 无意义。
几何上,切线和 $x$ 轴无交点。
-
无法收敛
- 越来越远离的不收敛。例如,$f(x)=x^{\frac{1}{3}}$ ,不论怎么选择起始点,$x_{n + 1} - x_n > 0$ ,下一个点比上一个点更远离根点 。
- 循环震荡的不收敛。
故应用该方法必须证明:
- 迭代式单调递减。
- 迭代式可以收敛于某点。(例如求$ f(x) = x^2 - n$ 时,需要证明迭代式收敛于$\lfloor\sqrt{n}\rfloor$)
Implementation
#include<iostream>
const int ep = 1e-12;
double getSquareRoot(double num) {
double x0, x1;
x0 = num;
x1 = (x0 + num / x0) / 2;
while (abs(x1 - x0) > ep) {
x0 = x1;
x1 = (x0 + num / x0) / 2;
}
return x1;
}
double getCubeRoot(double num) {
double x0, x1;
x0 = num;
x1 = x0 - (x0 * x0 * x0 - num) / (x0 * x0 *3);
while (abs(x1 - x0) > ep) {
x0 = x1;
x1 = x0 - (x0 * x0 * x0 - num) / (x0 * x0 *3);
}
return x1;
}
int main() {
double n;
std::cin >> n;
std::cout<<getSquareRoot(n);
std::cout<<std::endl;
std::cout<<getCubeRoot(n);
}
Proof
求$ f(x) = x^2 - n$ 时,迭代式为 $x_{i+1}-x_{i}=\left\lfloor\frac{1}{2}\left(x_{i}+\frac{n}{x_{i}}\right)\left\rfloor-x_{i}=\left\lfloor\frac{1}{2}\left(\frac{n}{x_{i}}-x_{i}\right) \right.\right.\right\rfloor$
- 显然,在区间 $[\sqrt{x},+\infty)$ 上,迭代式 $x_{i+1}-x_{i}$ 单调递减。
- 证明迭代式可以收敛至$\lfloor\sqrt{n}\rfloor$:
$$ x_{i+1}=\left\lfloor\frac{1}{2}\left(x_{i}+\left\lfloor\frac{n}{x_{i}}\right\rfloor\right)\right\rfloor=\left\lfloor\frac{1}{2}\left(x_{i}+\frac{n}{x_{i}}\right)\right\rfloor \geq\left\lfloor\frac{1}{2} \times 2 \times \sqrt{x_{i} \cdot \frac{n}{x_{i}}}\right\rfloor=\lfloor\sqrt{n}\rfloor $$